Total Variation regularization¶
This tutorial explains in detail how to use the Total Variation (TV) regularization in PyHST2. TV regularization is helpful for noise removal, features sharpening, limited data reconstruction ; and thus can improve further segmentations.
Consider the following slice of a simple dataset (Credits: ID11), reconstructed with standard Filtered Back-Projection (FBP) :
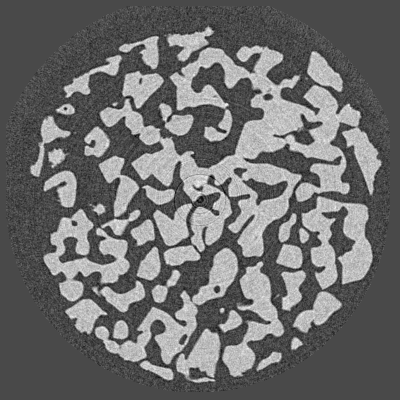
Slice reconstructed with FBP¶
This slice contains some noise and even small rings artifacts we want to get rid of. Regularization can be helpful. TV is especially adapted for this kind of slice, since it consists in few separated phases.
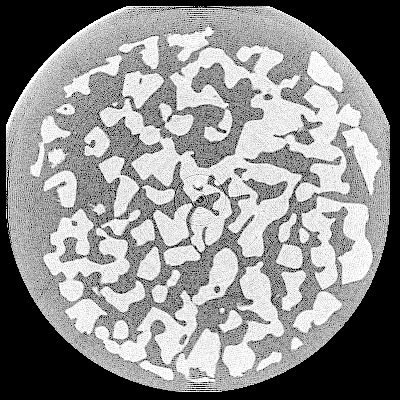
Let us start with a reconstruction with 300 iterations, and a regularization weight \(\lambda = 0.01\) :
ITERATIVE_CORRECTIONS = 300 # 300 iterations
DENOISING_TYPE = 1 # Total Variation regularization
OPTIM_ALGORITHM = 3 # Chambolle-Pock TV solver
BETA_TV = 0.01 # Regularization weight
We get the following result :
Slice reconstructed with TV regularization, \(\lambda = 0.01\)¶
If the regularization parameter \(\lambda\) is small, the solution is close to the solution of a least-squares formumation. Let us choose a bigger \(\lambda\) :
BETA_TV = 0.16
We get :
Slice reconstructed with TV regularization, \(\lambda = 0.16\)¶
The result is better. The rings artifacts have disappeared, and the noise is attenuated in the sample, making the segmentation easier.
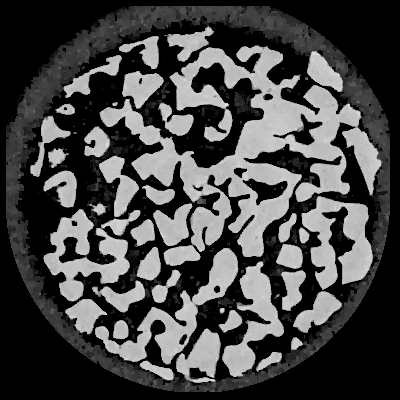
Now, if \(\lambda\) value is too high, the result will be a piecewise-constant image :
BETA_TV = 5.0

Slice reconstructed with TV regularization, \(\lambda = 5.0\)¶
The value of BETA_TV has to be tuned for the best reconstruction.
You can reconstruct a single slice with different values of BETA_TV and see what is the best result.
The optimum value depends on the dataset : signal to noise ratio, data completeness, data scale, features you want to see, …
Finding the best BETA_TV is a tradeoff between least-squares solution (FBP-like reconstruction) and cartoon-like solution (too much regularization).
- The typical process of parameters tuning is the following :
Tune
ITERATIVE_CORRECTIONSto determine the number of iterations. If this value is too small, the algorithm will not provide the “converged” solution. On the other hand, a too high value produces useless iterations. The convergence indicator is the energy displayed in thestdout. A typical value, when the preconditioner is enabled, is 1000 iterations for FISTA and 500 for Chambolle-Pock.Tune
BETA_TVto have a less “noisy” reconstruction while preserving the features.