Debye Waller Factors Calculation

The script make_TDS_DW create the DW factors for a given temperature. The script does an integral sum over the whole Brillouin zone using previous knowledge of the dynamical matrix that has been obtained, through make_TDS_Simmetrization. The output is written into the hdf5 file associated to the castep output file.

  • The usage is

    make_TDS_DW castep_filename input_filename

    the file castep_filename can be either the name of the original castep output our the associated hdf5 file. In any case the associated hdf5 file must exist already (make_TDS_Simmetrization must be runned beforehand )

  • The input_file must set the variables :

    • TEMPERATURE
    • APPLYTIMEREVERSAL

    using a python syntax

The input variables are documented with docstrings below

make_TDS_DW.APPLYTIMEREVERSAL = 1
  • write APPLYTIMEREVERSAL=1 in input file to duplicate eigenvectors at K to get those at -K by complex conjugation
  • write APPLYTIMEREVERSAL=0 otherwise
make_TDS_DW.Temperature = 100.0

The temperature at which DW factors are calculated. Units are Kelvin

TDS_Simmetry.CalcDWatT(Temperature, calculatedDatas, filename=None, md5postfix=None, overwrite=False, key=None, MAKING=0, simmetries_dict=None)[source]

The Debye-Waller coefficients are calculated atom by atom. For each atom they consist in a 3X3 matrix :

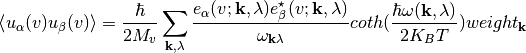
\left< u_{\alpha}(v) u_{\beta}(v) \right> = \frac{\hbar}{2 M_v } \sum_{ {\bf k},\lambda} \frac{e_{\alpha}(v;{\bf k},\lambda) e^{\star}_{\beta}(v;{\bf k},\lambda) } {\omega_{{\bf k} \lambda}} coth(\frac{\hbar \omega({\bf k},\lambda)}{2 K_{B} T}) weight_{{\bf k}}

where the sum of weigths is one (weigths are given by ab-initio griding).

The Debye-Waller factors are given in atomic units. Internally the routine takes temperature in Kelvin and converts it to Hartree, while the eigenvetors e are dimensionles, the frequencies calculated from the ab-initio dynamical matrix are given in units of 1/cm and are converted also to Hartree