Fourier Interpolation of the dynamical matrixΒΆ

This script calculates Fourier Transform of the dynamical matrix.

  • The usage is

    make_TDS_Fourier castep_filename input_filename

    the file castep_filename can be either the name of the original castep output or the associated hdf5 file. In any case the associated hdf5 file must exist already: make_TDS_Simmetrization must have been run beforehand in order to fill by symmetry operations the missing part of the Brillouin zone. The Fourier transform is performed by summing over the whole Brillouin zone the periodic dynamical matrix

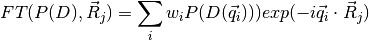
    FT(P(D), {\vec R_j}) = \sum_i w_i P(D{(\vec q_i}))) exp( -i {\vec q_i}\cdot {\vec R_j})

    where i runs over all provided q-points (the original and the simmetry-replicated ones). The vectors R_j are defined in real space on the Bravais lattice of the crystal.

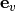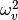    The Dynamical matrix is defined in periodic notation in Q space. It is obtained on the basis of eigenvectors {\mathbf e_v} and eigenvalues \omega^2_v:

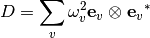
    D = \sum_v \omega^2_v {\mathbf e_v} \otimes {\mathbf e_v}^\ast

    provided by the input file. If the eigenvectors are periodic in 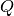Q the matrix is already periodic, but often, as it is the case for castep, the natural choice is outputting Bloch-Theorem satisfying vectors. In this latter case the periodicity of the dynamical matrix is ensured by adding/removing the proper phases.

  • The input_file must set the variables:

    • Nfour_interp
      this variable is very important. The cubic grid counts 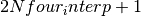2 Nfour_interp + 1 points along each primitive Bravais axis. This number must be large enough to exceed the spatial range of the forces in order to cope with the variation of the Dynamical matrix: the longer the interaction distance, the higher the necessary Nfour_interp will be. A too large Nfour_interp may however cause artefacts. In this case either you have to lower it, or if it is really necessary to keep long distance interactions you have to increase the number of calculated q-points in the input file.
    • APPLYTIMEREVERSAL

    using a python syntax

The input variables are documented with docstrings below

make_TDS_Fourier.APPLYTIMEREVERSAL = 1

this is one by default. Must be coherent with previous steps

make_TDS_Fourier.Nfour_interp = 5

The number of points in each direction of the 3D reciprocal grid